
Circles and Triangles
Above: Solving for x²+y² = r² . Nodes used: I created two number sliders for variables - (Radius & Adjacent side), along with an expression evaluate node, square root node and vector node for XYZ.
Above: I created a variable for the radius of pivot circle and multiplied it *2 to find the center point distance of the orbiting circle. I input the arc variable as radians - rad(x).
Note: Input for expressions = x
Above: I added a 2nd circle with the expression Acos(1/2) and added the Arc variable to it. Note that the corresponding angle is 60° .

Unit Circle reference image above from: Inverse Trigonometric/ArcCos.
I added more circles.
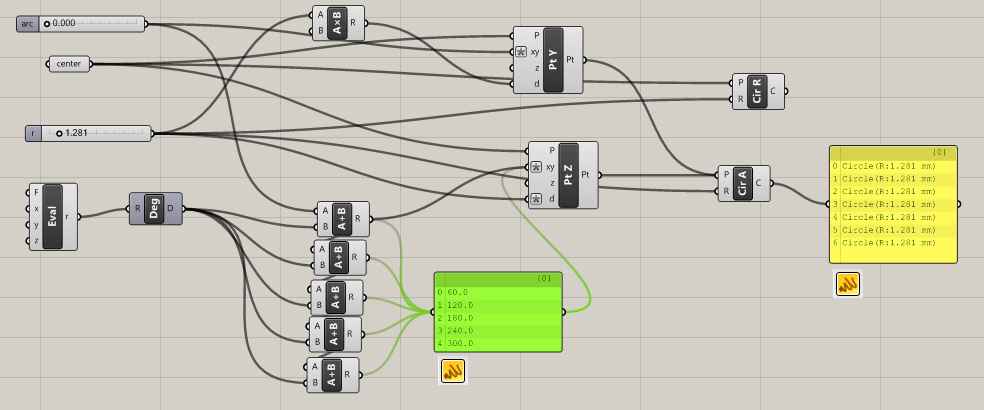
Above: By shift dragging connections we can connect multiple links and post-it note style lists help visualize inputs/outputs. We could also use the merge node.
Function Curves
Construct Domain node (DOM) - Start Value (-10) End Value (10) (= -10 to 10)
Range Node - Give domain (-10 to 10) and steps (creates even spacing for steps within the domain - for example 10 will give a list of steps each at 1/10th the domain).
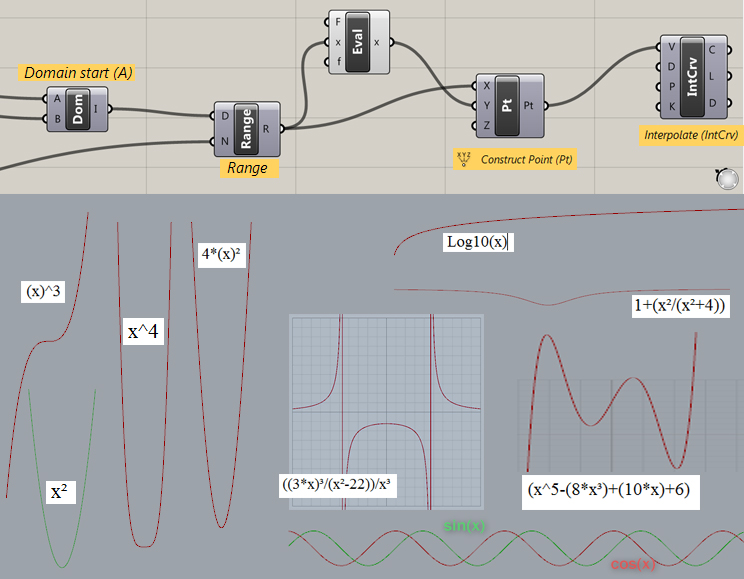
Interesting use of expressions for curves - see this article. I input a variety of variables, as number sliders, to create these pretty patterns.
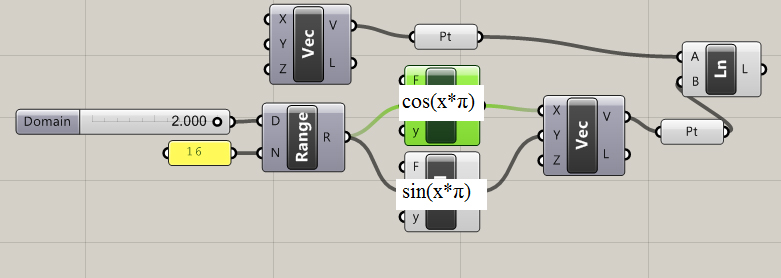
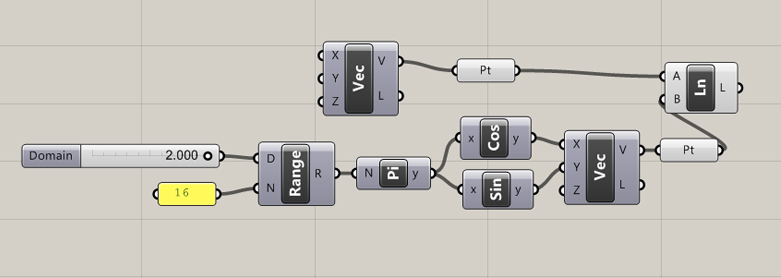
2 π = 360 degrees. 1 π = 180 degrees. I created two expressions, (cos(x* π) and sin(x* π), as vectors x and y to simulate the unit circle. The range node automatically generates a 10 number list within a domain (D). When we set the domain to 2 (2 π) we get a complete rotation of our unit circle. It works the same way with a node tree instead of an expression.
Pappus Chain
First I set up a simple relationship between three circles. As the radius of one circle increases the other decreases respectively. The magnitude of each vector also increases or decreases to offset the change in radius . All three circles remain tangent.
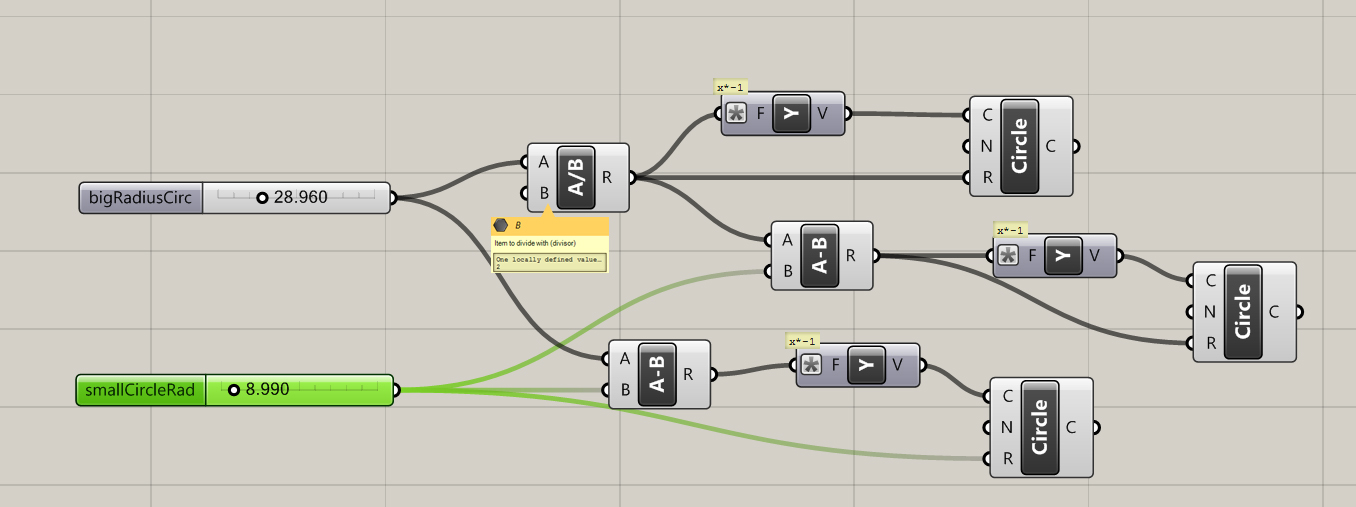

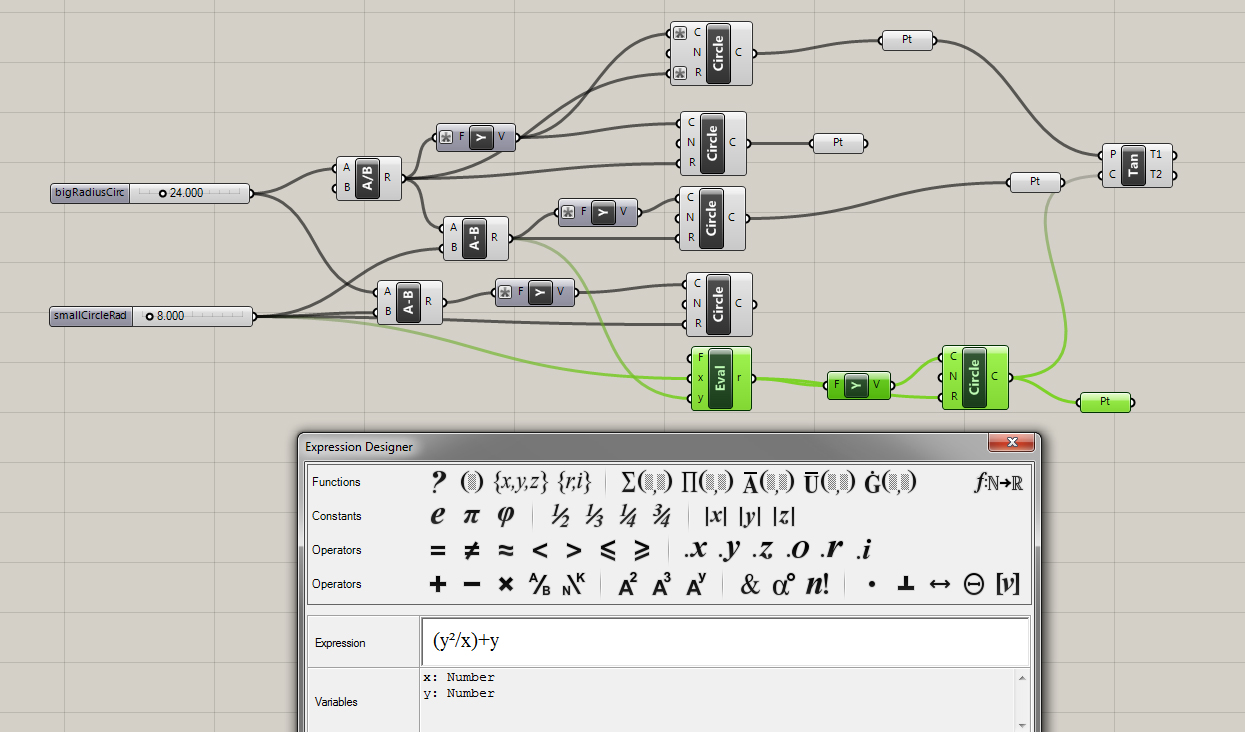
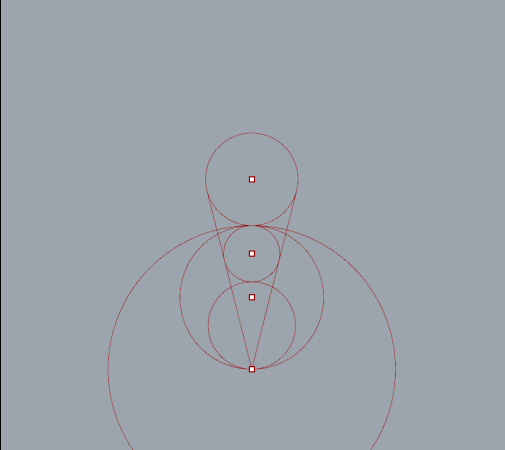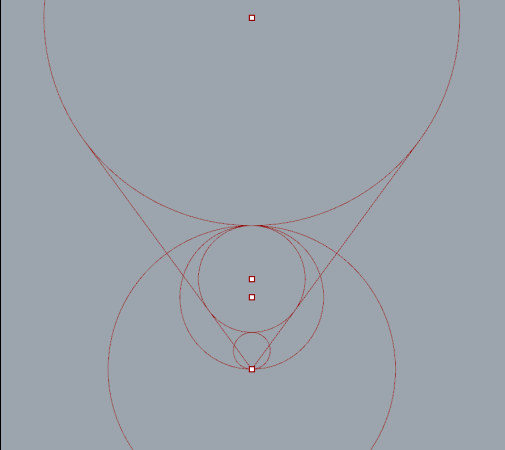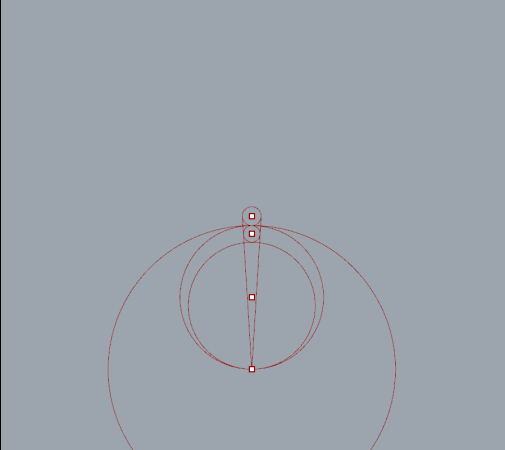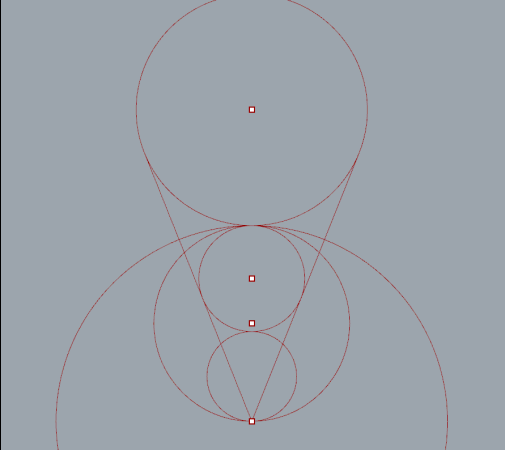
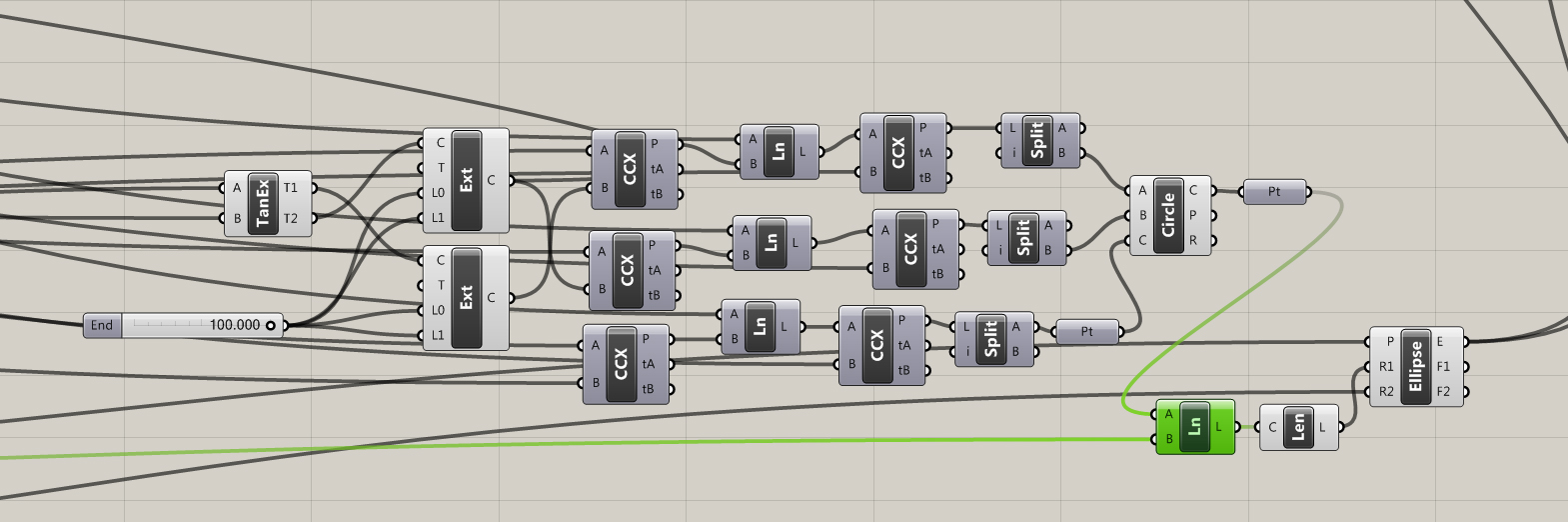
By extruding a number of tangent lines I was able to extract the necessary points using the curve|curve tool. Split nodes, set to integer 1, were needed to split the list generated when more then one intersection occurred.
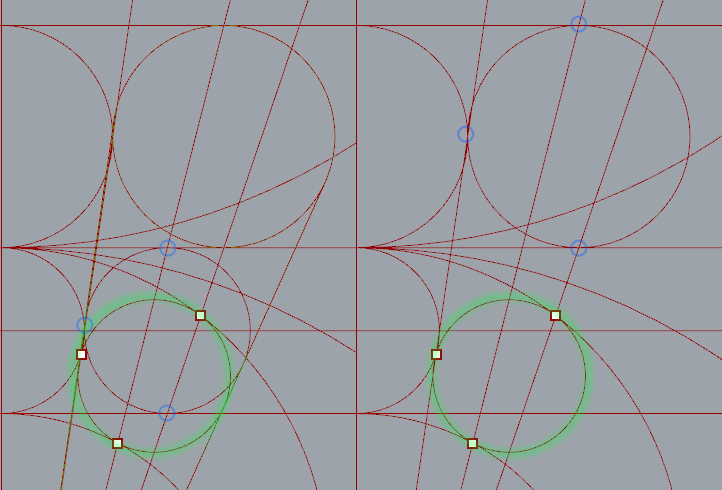

Circle number 2 added. Interesting but not very practical.
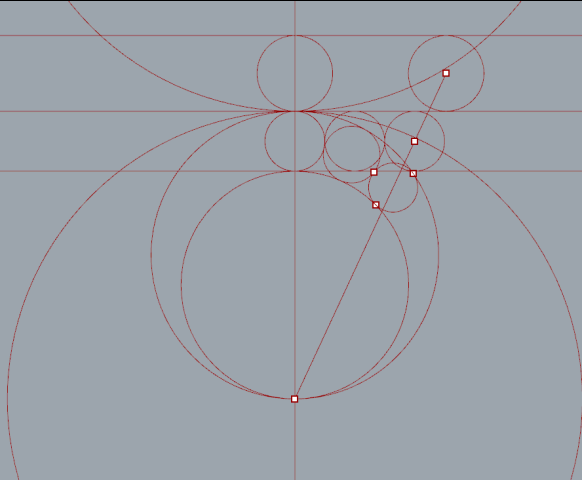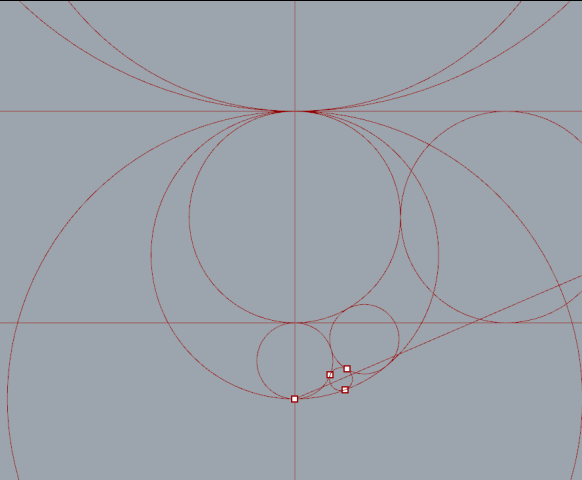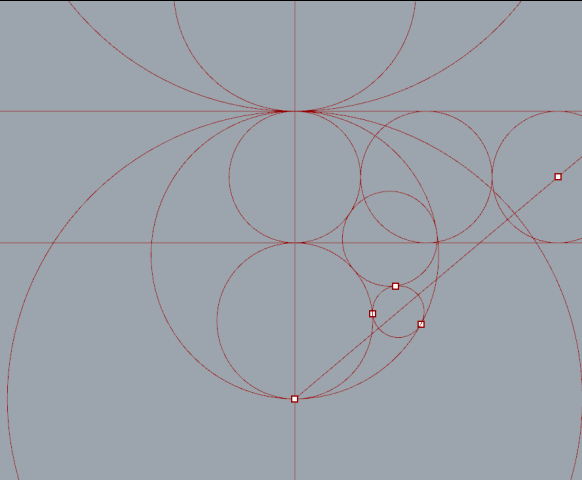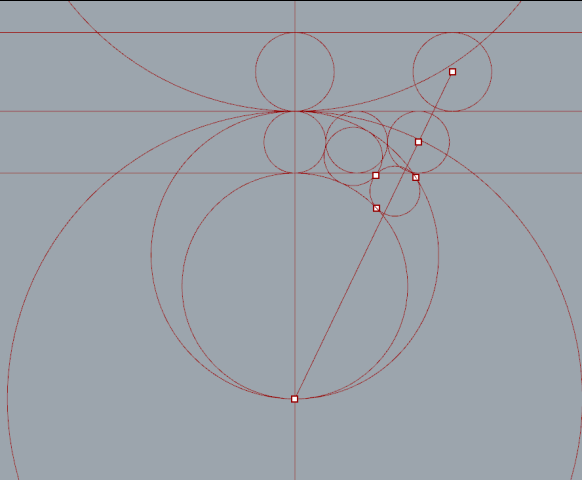


"Series" nodes iterate versions of the top circle with 2*radius for steps. Lines from each circles center point intersect with the ellipse.
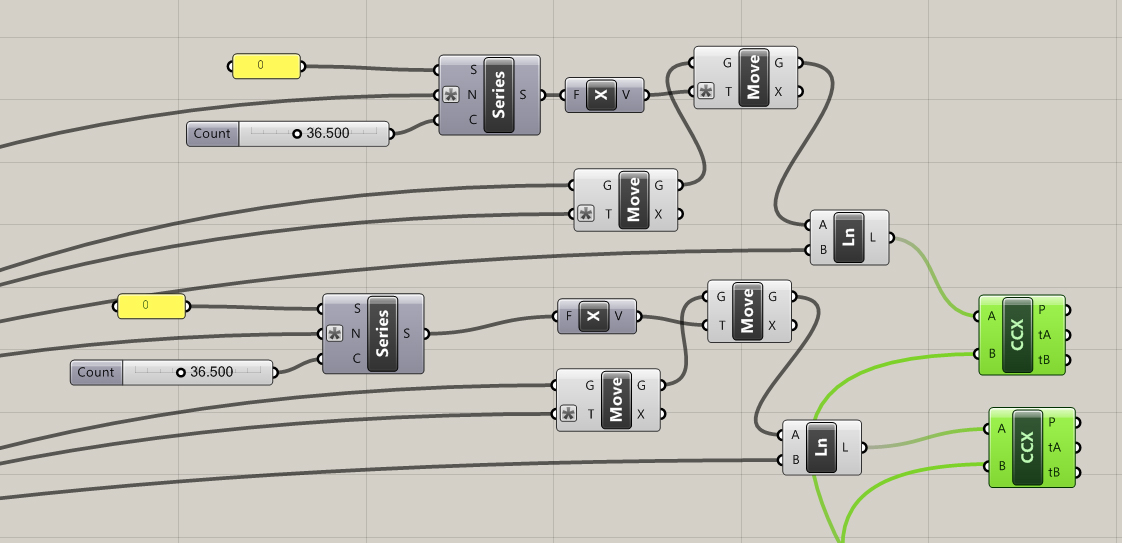
There are a bunch of interesting articles about the Pappus Chain. It would be a lot of fun to dive in more deeply and explore the mathematics properly. It's a very interesting subject. See links...
Reuleaux SkyscraperIt seems that everyone who uses Grasshopper for Rhino builds a skyscraper first. So why not. I'll try a simple mathematical shape - A Reuleaux Triangle. It's an interesting enough shape.
"Rotation of a Reuleaux triangle within a square, showing also the curve traced by the center of the triangle"
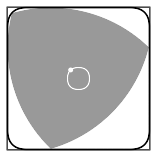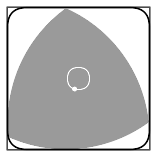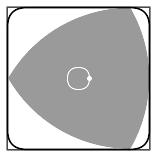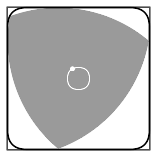
A Reuleaux Triangle is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two.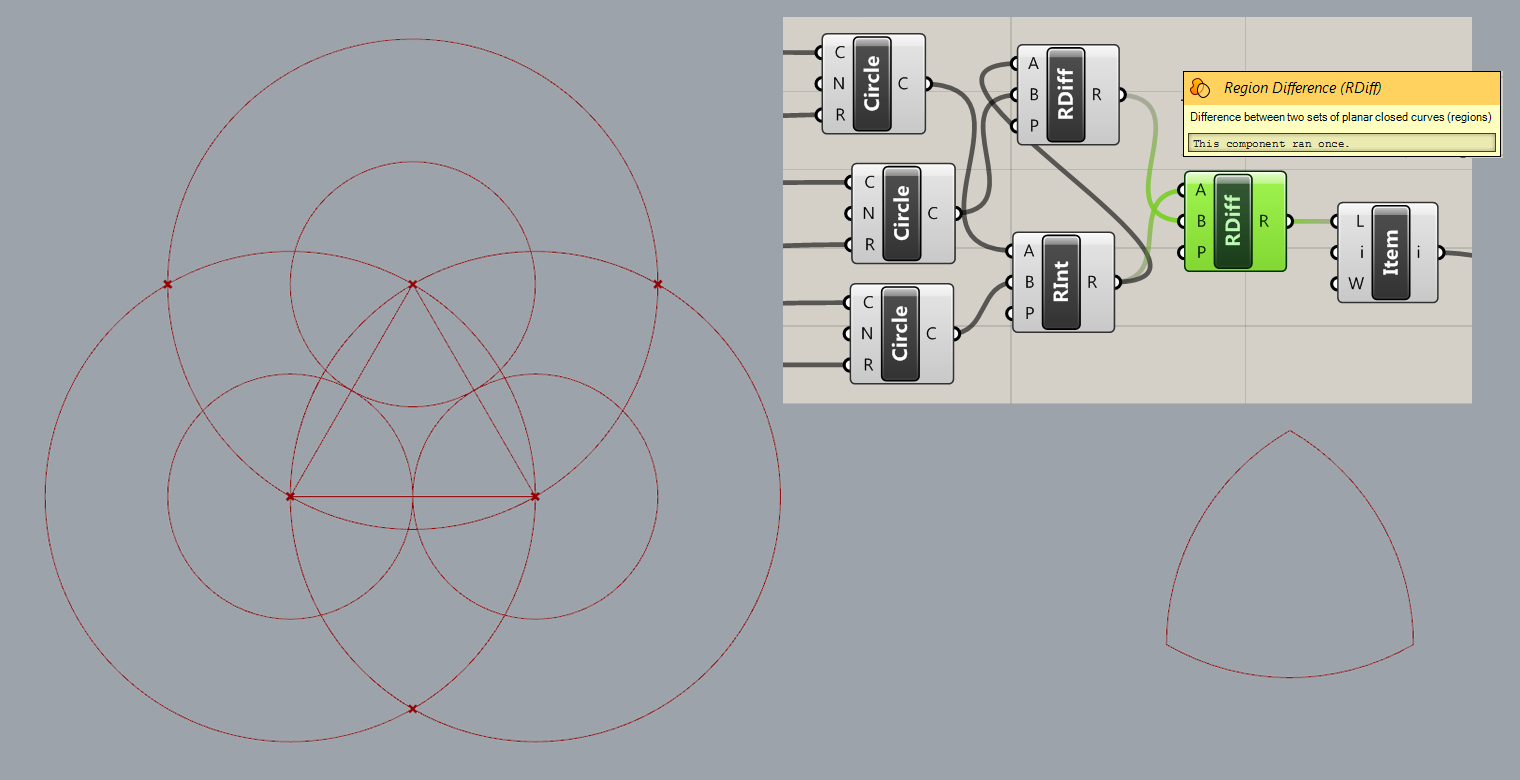
Above: Before and after trim using region difference nodes to extract the reuleax triangle shape.
Twisting Node tree tests
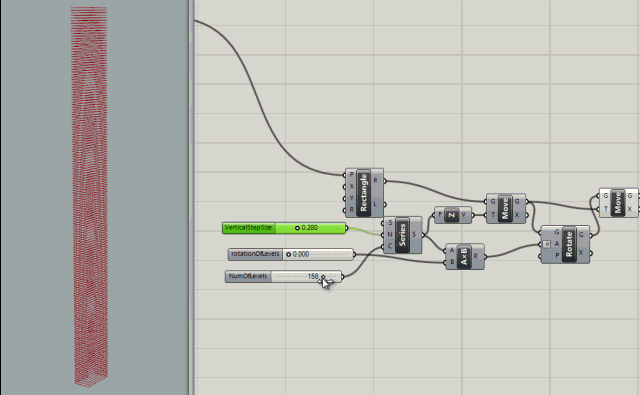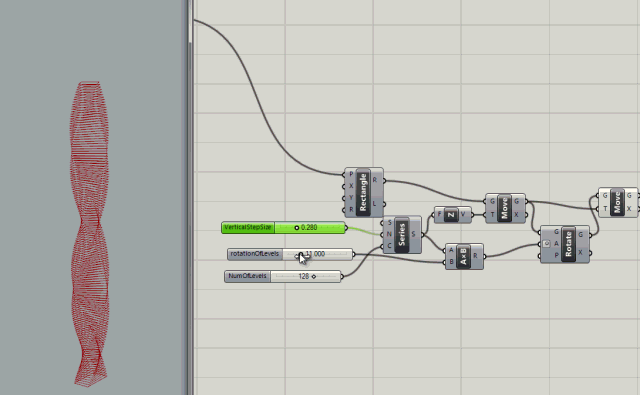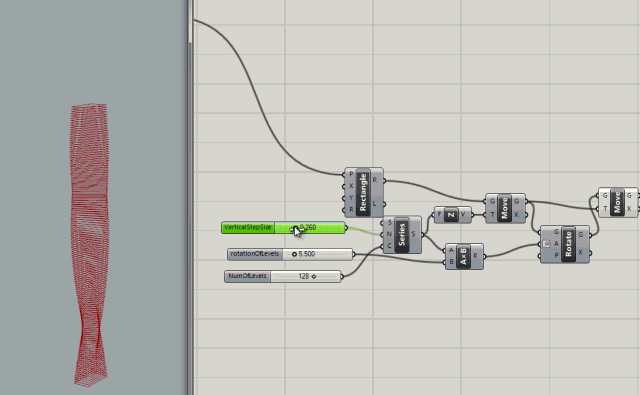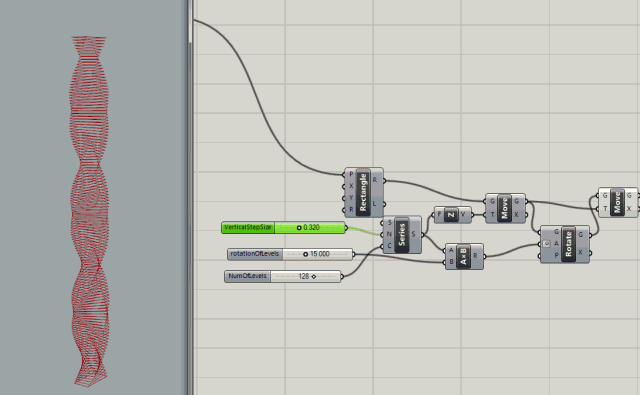
Series node with inputs to control the count (number of levels), the rotation of levels (in degrees), and the step size (size between levels)
.

More control added with rotation variables for rotating the the start and end of the building.
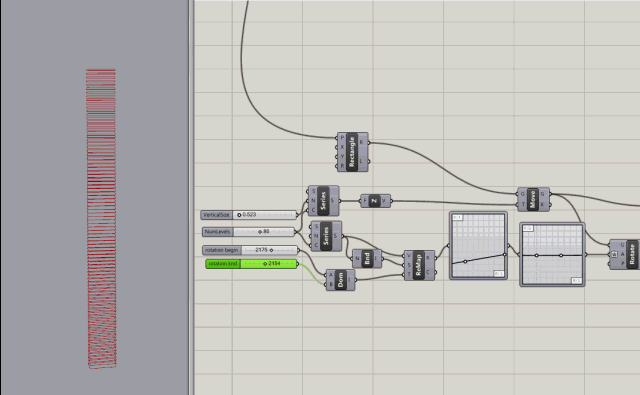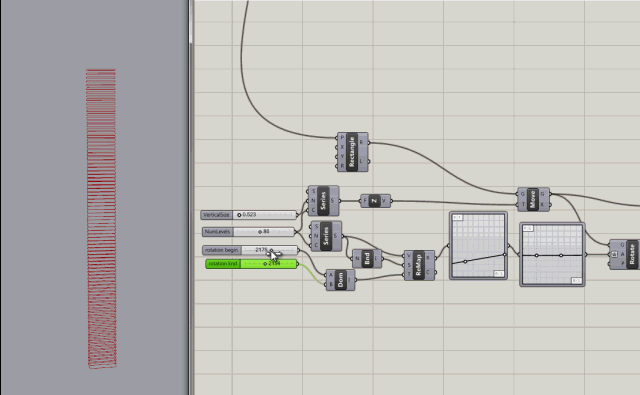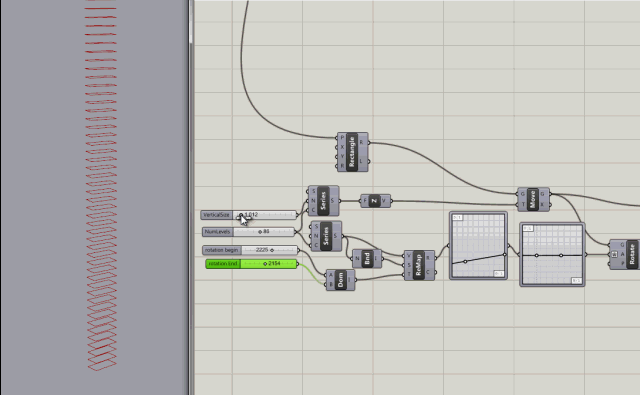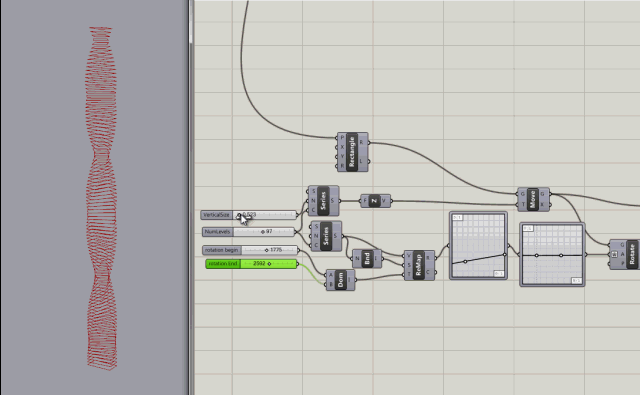

After a little more reading, and watching some youtube tutorials, I created my first grasshopper building. Not very interesting but it doesn't have to be. Its just for learning.


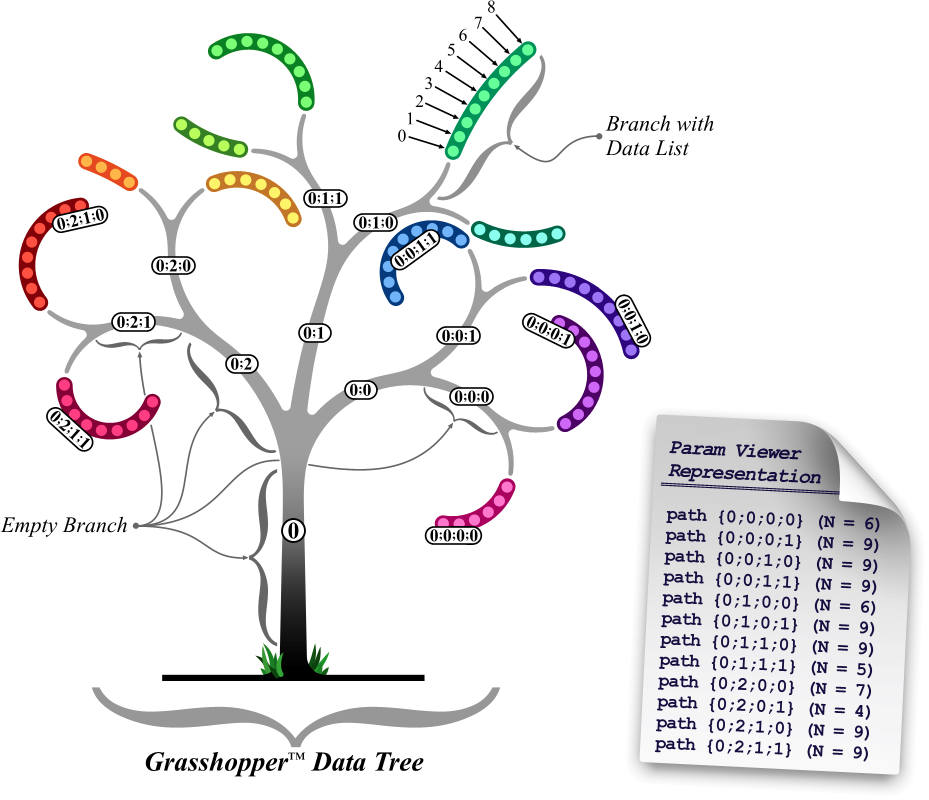
The node tree can be visualized with a param Viewer node which can display the tree visually - see node tree image.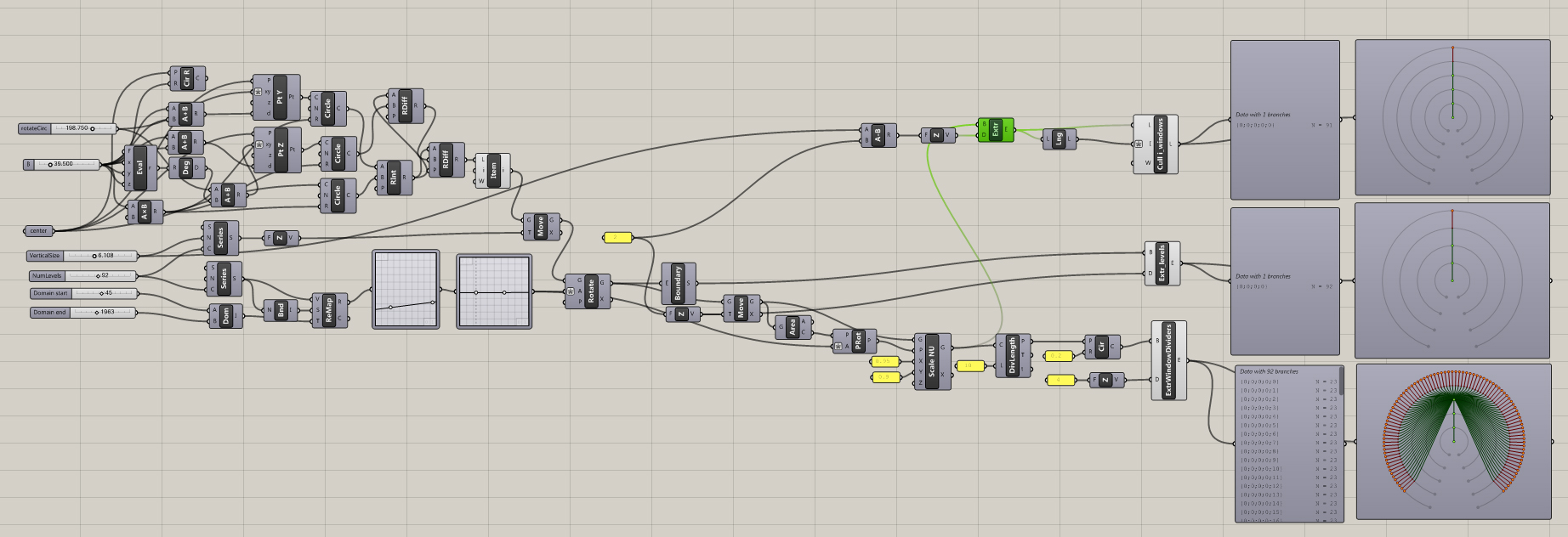

Grasshopper creator, David Rutton, has a video about data trees here.
To be continued...

















No comments:
Post a Comment