Apartment Block - Modeling Practice

Base shape (mirrored)

Level Shape (mirrored)

25 Levels

Looking up

Metallic Carpenter Bee (Xylocopa (Lestis)) - Poly Modeling

A screen capture of my poly modeling session - the old fashioned way.

Initial tests for the Iridescent Bee Shader
First something super simple - Fall off curves for red green and blue. I was trying to match some photo reference of an iridescent beetle - reference image sourced from here - HERE

 

Second - a test render using "Thin Film Interference". This is a work in progress but I like the general direction its going. More hair and some modeling tweeks are obviously needed. Photos of the actual bees can be found HERE. They're quite pretty. 

Shader test renders:

Wires:

 To be continued...

First Experiments using Grasshopper for Rhino

Grasshopper for Rhino – visual programming language/environment
 

This is a blog post of notes made whilst using Grasshopper for the first time.
Circles and Triangles

Above: Solving for x²+y² = r² . Nodes used: I created two number sliders for variables - (Radius & Adjacent side), along with an expression evaluate node, square root node and vector node for XYZ.

Above: I created a Theta variable and plugged it into the Cosine(sideX) and Sine(sideY) functions, as degrees, and then into a Vector XYZ node. Math revision - SohCahToa

Above: Cos and Sin multiplied by radius.

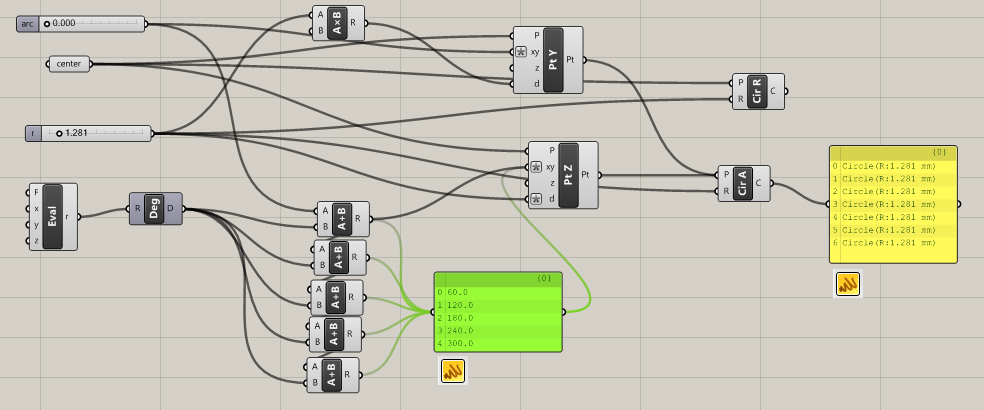
Above: I created a variable for the radius of pivot circle and multiplied it *2 to find the center point distance of the orbiting circle. I input the arc variable as radians - rad(x).  
Note: Input for expressions = x

Above: I added a 2nd circle with the expression Acos(1/2) and added the Arc variable to it. Note that the corresponding angle is 60° .

Unit Circle reference image above from: Inverse Trigonometric/ArcCos.

I added more circles.

 

Above: By shift dragging connections we can connect multiple links and post-it note style lists help visualize inputs/outputs. We could also use the merge node.

Function Curves 

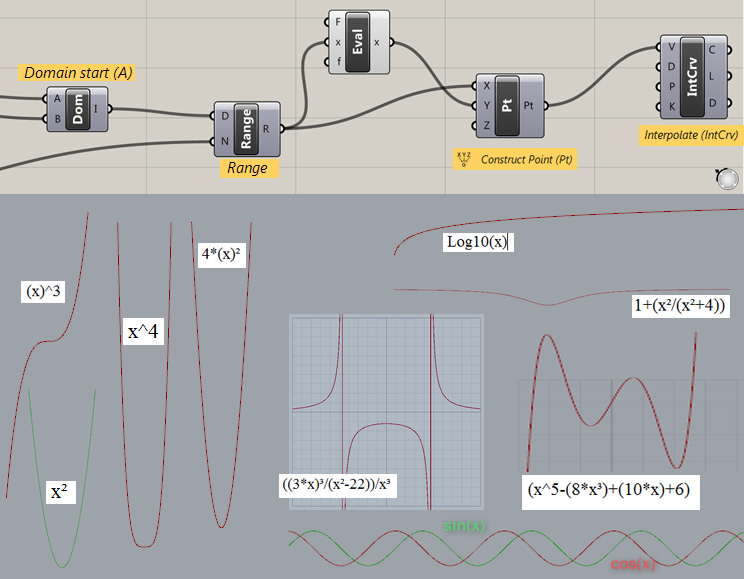
Construct Domain node (DOM) - Start Value (-10) End Value (10) (= -10 to 10) 

Range Node - Give domain (-10 to 10) and steps (creates even spacing for steps within the domain - for example 10 will give a list of  steps each at 1/10th the domain).

 

Interesting use of expressions for curves - see this article. I input a variety of variables, as number sliders, to create these pretty patterns.

Unit circle
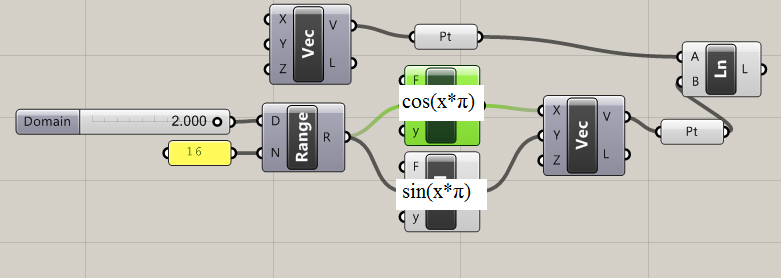
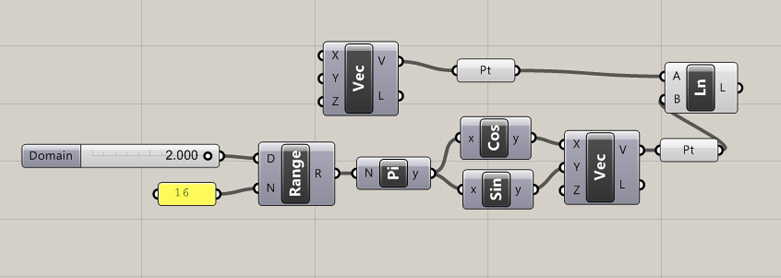
2 π = 360 degrees. 1 π = 180 degrees. I created two expressions, (cos(x* π) and sin(x* π), as vectors x and y to simulate the unit circle. The range node automatically generates a 10 number list within a domain (D). When we set the domain to 2 (2 π) we get a complete rotation of our unit circle. It works the same way with a node tree instead of an expression.

 

 

Pappus Chain 

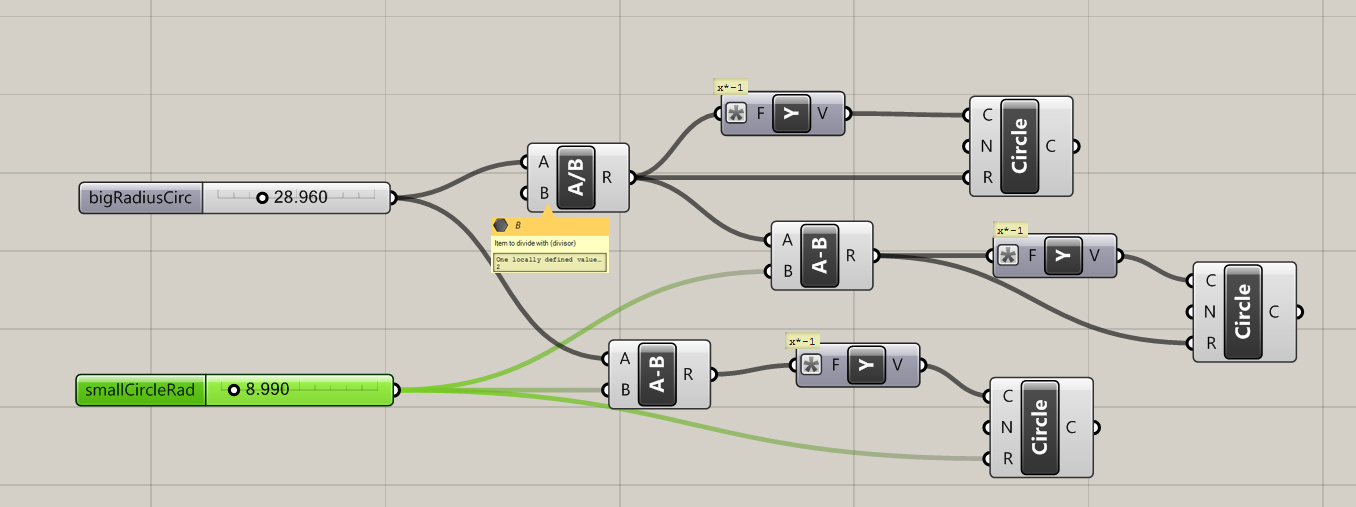
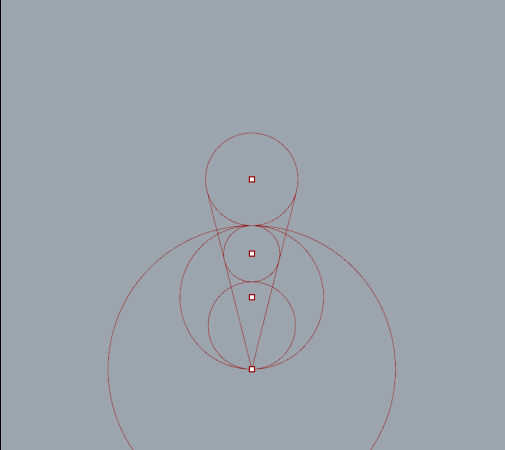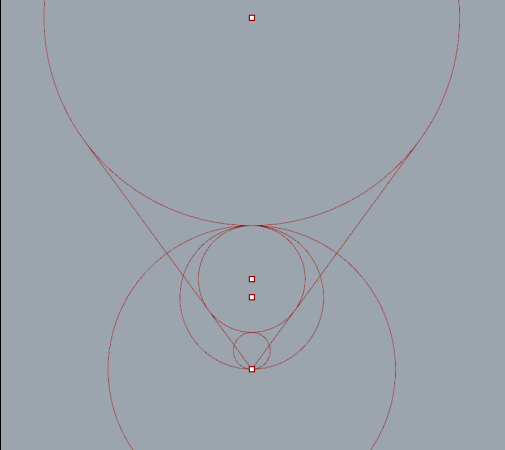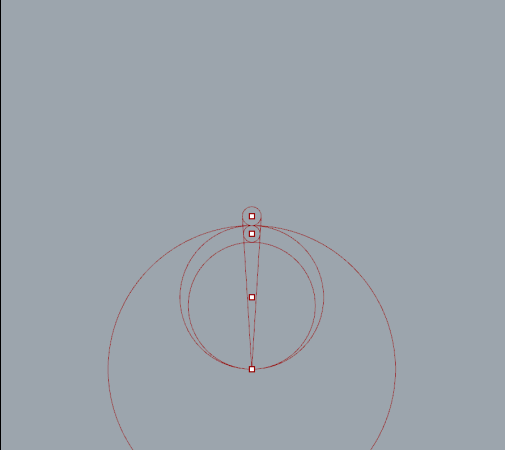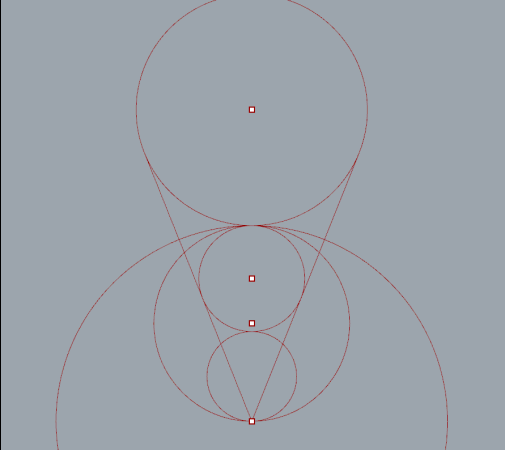
First I set up a simple relationship between three circles. As the radius of one circle increases the other decreases respectively. The magnitude of each  vector also increases or decreases to offset the change in radius . All three circles remain tangent.

 

 

Next I wrote an expression to invert the top circle and tested it with some tangent lines.

 

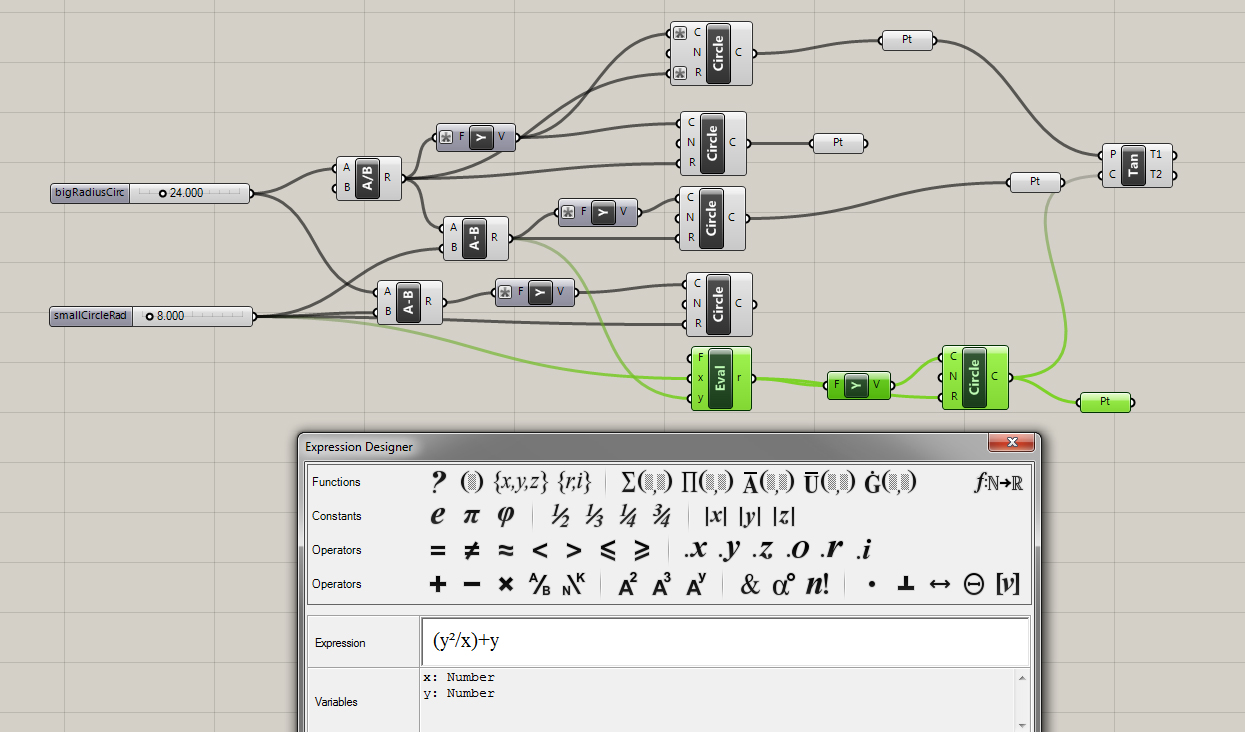
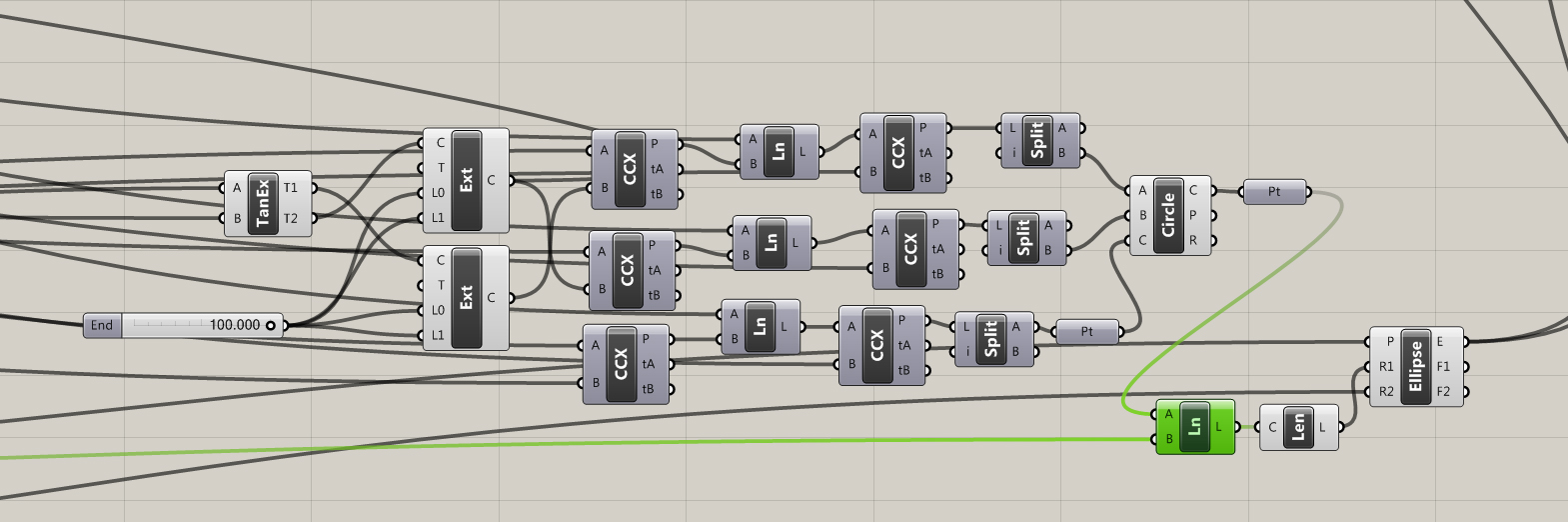
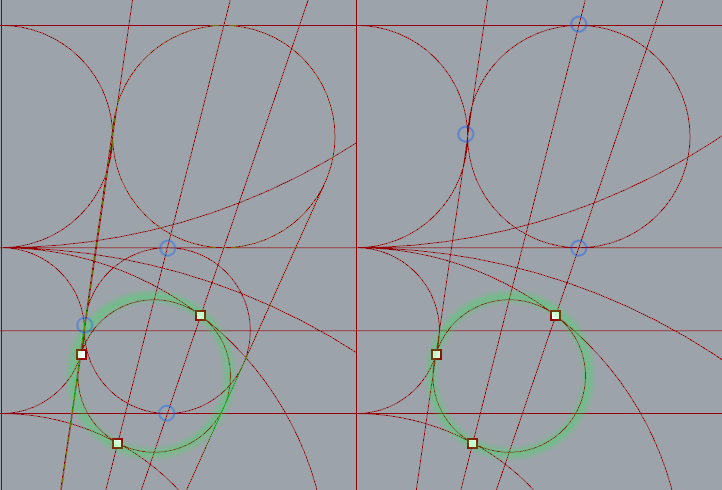
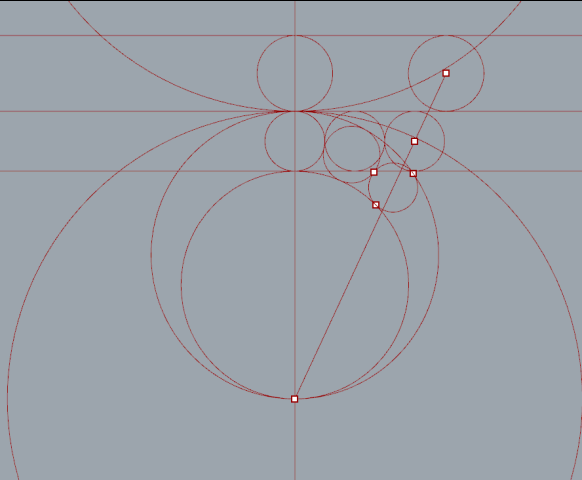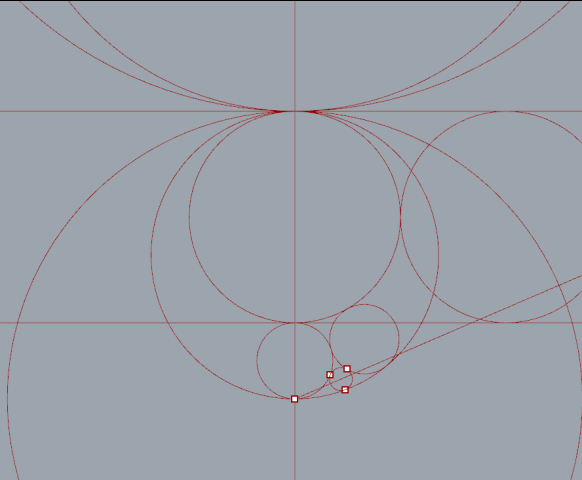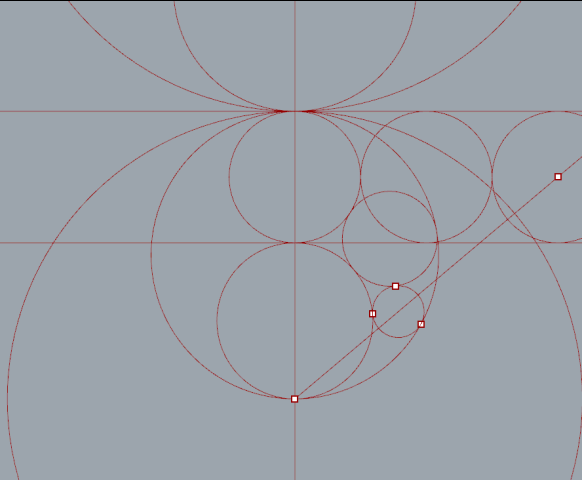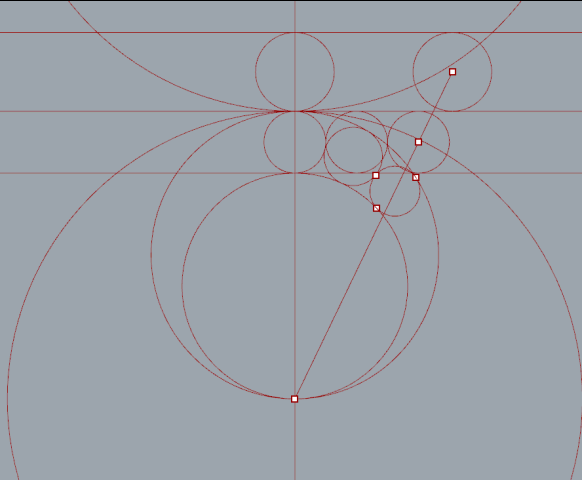
After a little bit of reading I found a number of ways to place the chain of circles. The most direct way is to calculate a three point circle from intersection points.

By extruding a number of tangent lines I was able to extract the necessary points using the curve|curve tool. Split nodes, set to integer 1, were needed to split the list generated when more then one intersection occurred.

 

 

 

Circle number 2 added. Interesting but not very practical.

With one circle created there is enough information to generate an ellipse. Math Revision - x²/a² + y²/b² =1

More circles added.

"Series" nodes iterate versions of the top circle with 2*radius for steps. Lines from each circles center point intersect with the ellipse.

 

There are a bunch of interesting articles about the Pappus Chain. It would be a lot of fun to dive in more deeply and explore the mathematics properly. It's a very interesting subject. See links...

Epic Circles - Numberphile

Pappus Chain - Wolfram - Math World

Arbelos

Steiner Chain

Wiki - Pappus Chain

Chain Reaction

Reuleaux Skyscraper
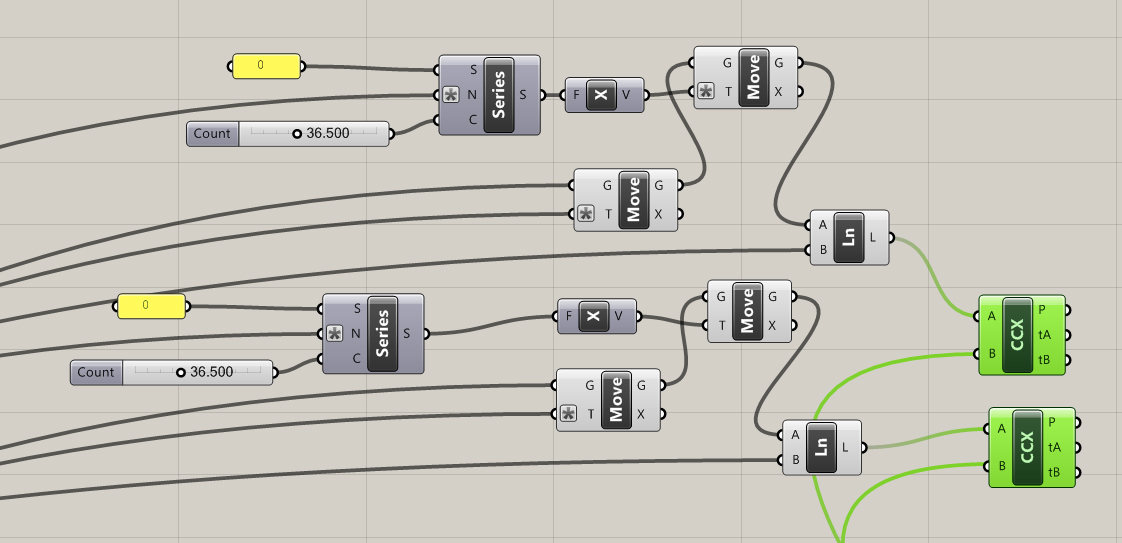
It seems that everyone who uses Grasshopper for Rhino builds a skyscraper first. So why not. I'll try a simple mathematical shape - A Reuleaux Triangle. It's an interesting enough shape.

"Rotation of a Reuleaux triangle within a square, showing also the curve traced by the center of the triangle"

See Wikipedia entry

A Reuleaux Triangle is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two.

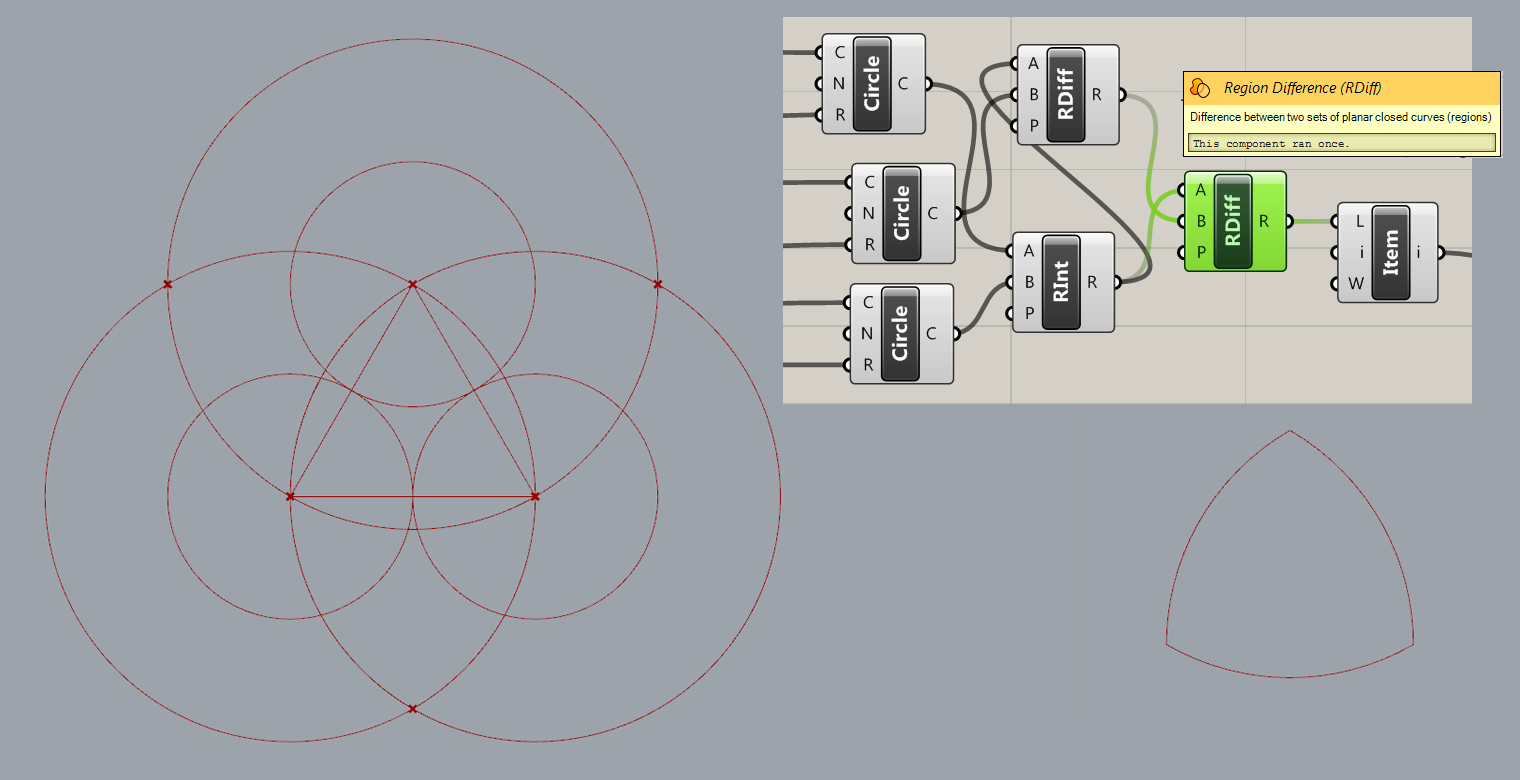
Above:  Before and after trim using region difference nodes to extract the reuleax triangle shape.

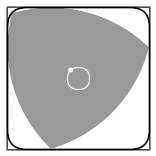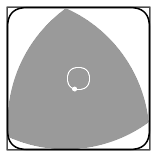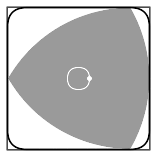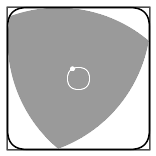
Twisting Node tree tests

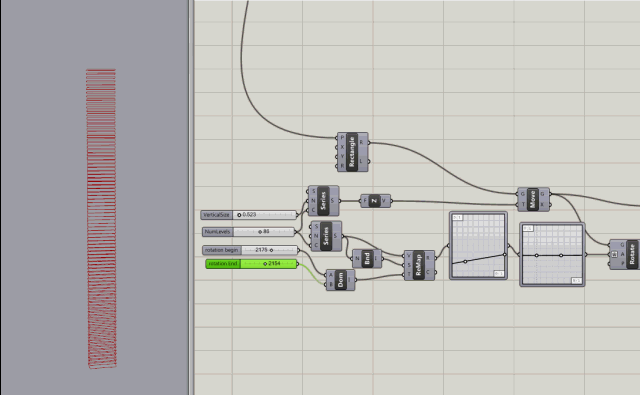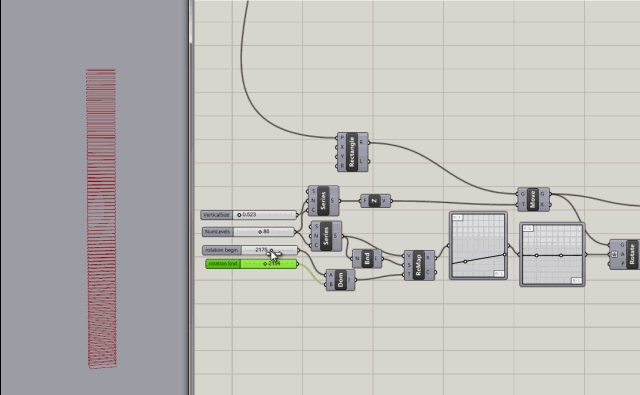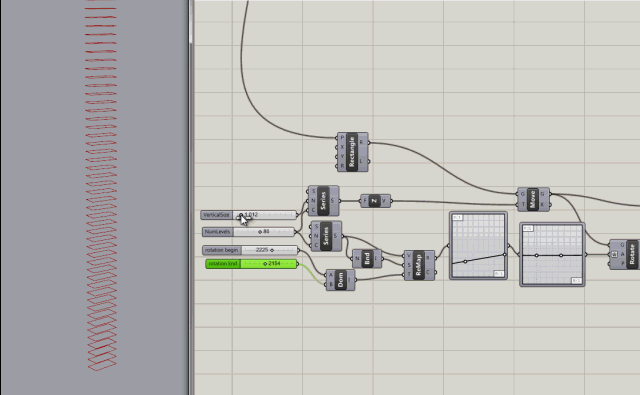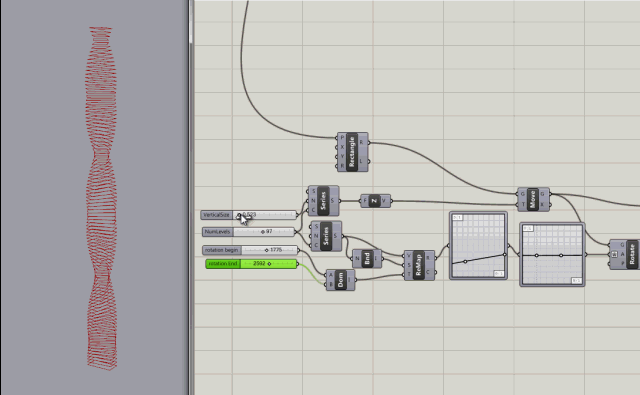
Series node with inputs to control the count (number of levels), the rotation of levels (in degrees), and the step size (size between levels)

.

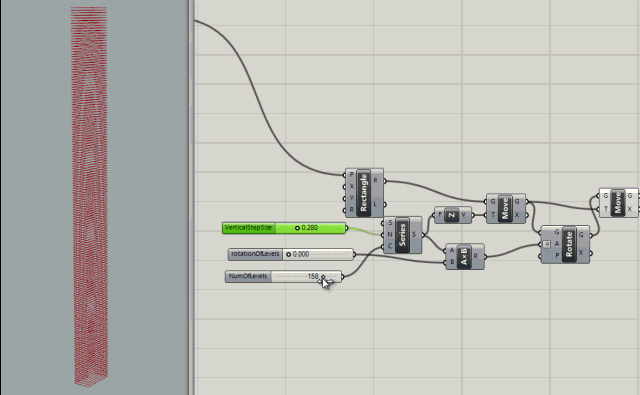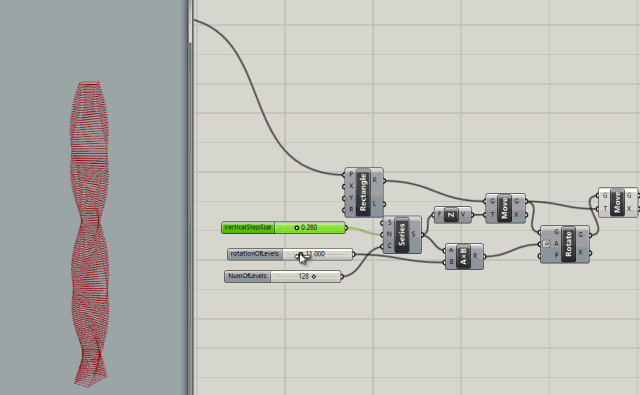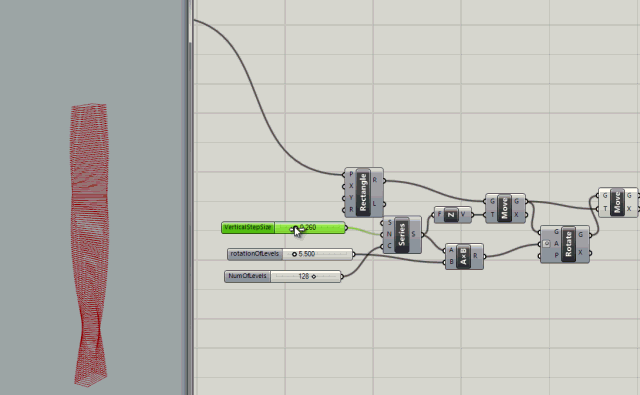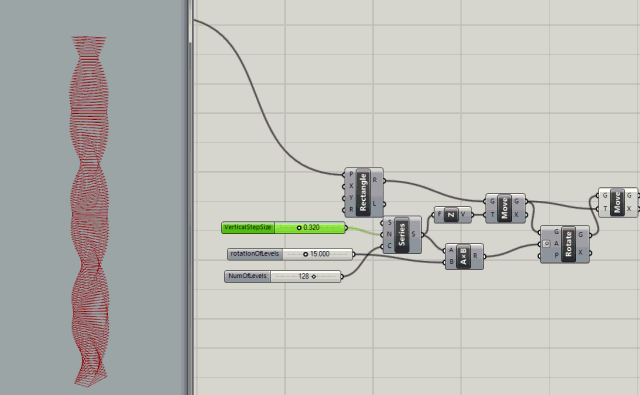
More control added with rotation variables for rotating the the start and end of the building.

After a little more reading, and watching some youtube tutorials, I created my first grasshopper building. Not very interesting but it doesn't have to be. Its just for learning.

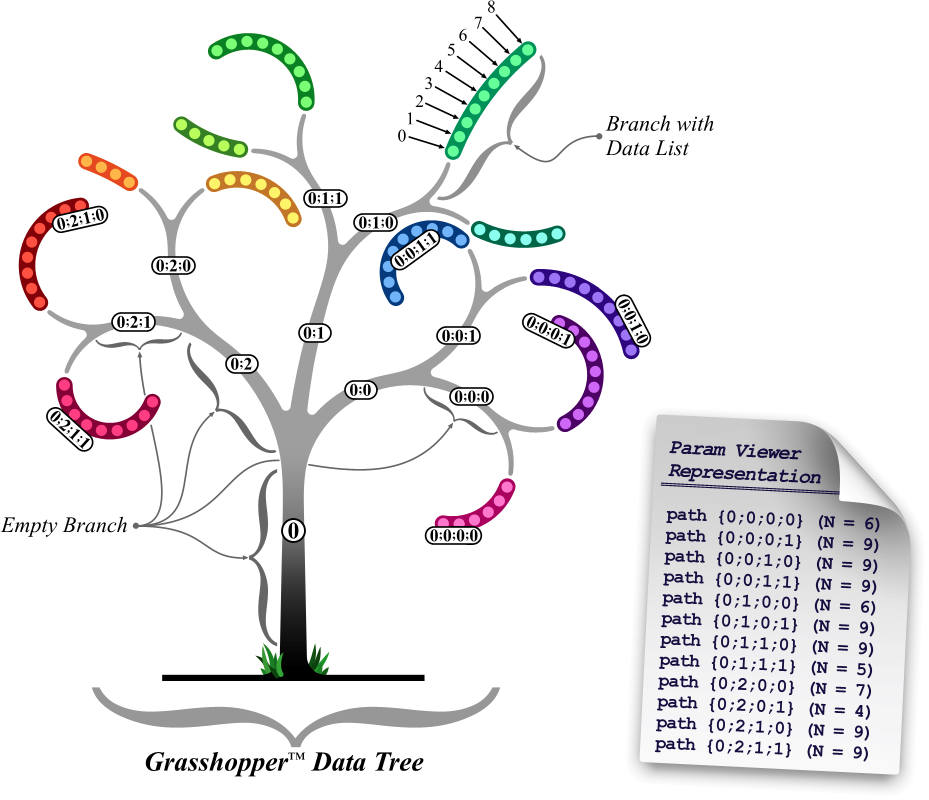
The node tree can be visualized with a param Viewer node which can display the tree visually - see node tree image.

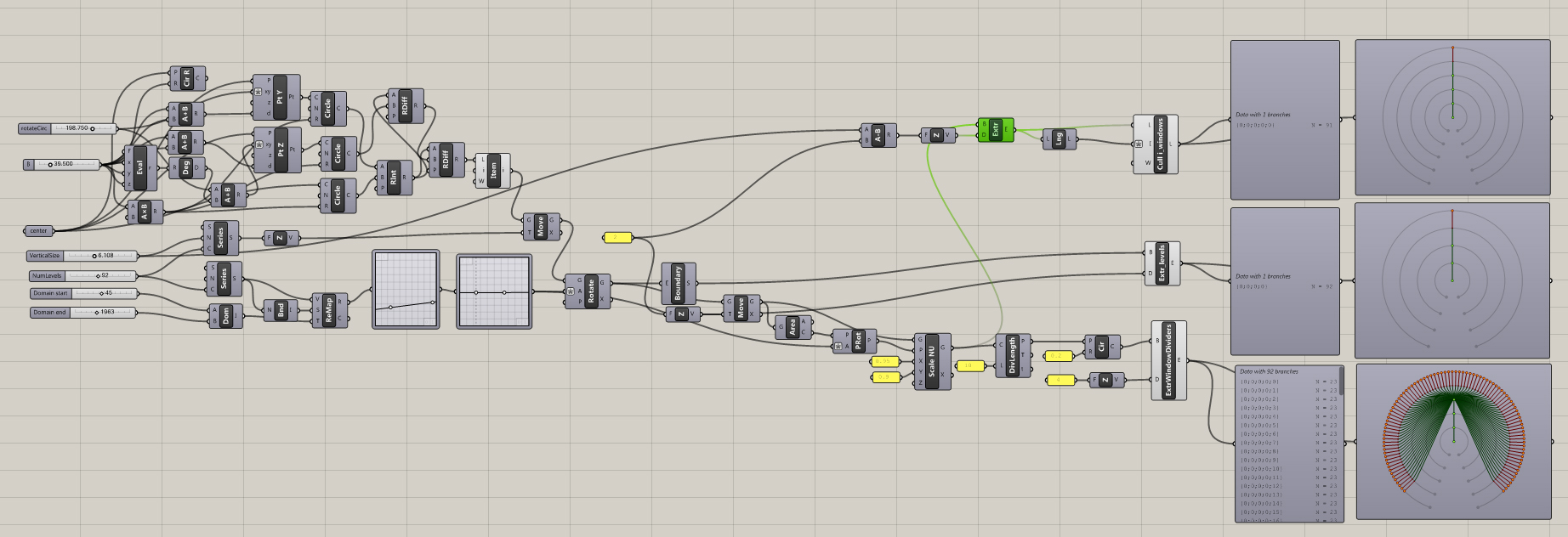
Grasshopper creator, David Rutton, has a video about data trees here.

Nodes of note for data manipulation/deconstruction:

 To be continued...